Gradient Informed Proximal Policy Optimization

Abstract

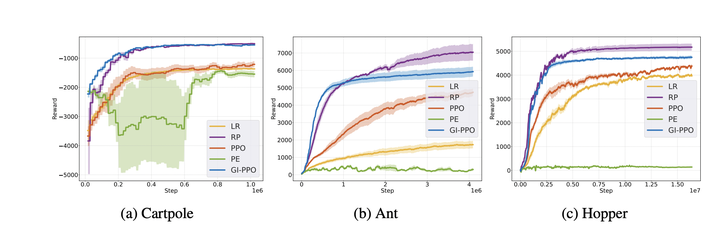
We introduce a novel policy learning method that integrates analytical gradients from differentiable environments with the Proximal Policy Optimization (PPO) algorithm. To incorporate analytical gradients into the PPO framework, we introduce the concept of an α-policy that stands as a locally superior policy. By adaptively modifying the α value, we can effectively manage the influence of analytical policy gradients during learning. To this end, we suggest metrics for assessing the variance and bias of analytical gradients, reducing dependence on these gradients when high variance or bias is detected. Our proposed approach outperforms baseline algorithms in various scenarios, such as function optimization, physics simulations, and traffic control environments. Our code can be found