Learning on 3D Meshes with Laplacian Encoding and Pooling

Abstract

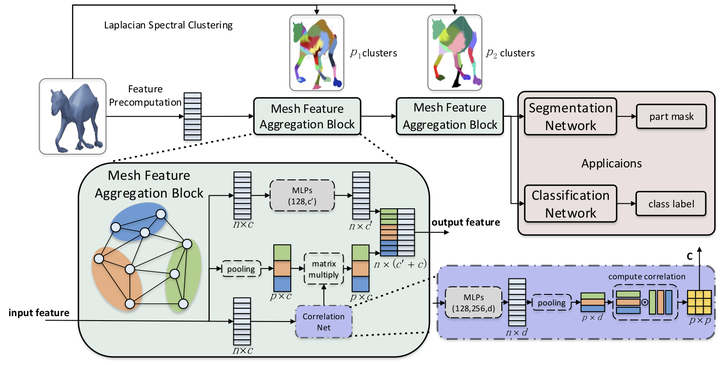
3D models are commonly used in computer vision and graphics. With the wider availability of mesh data, an efficient and intrinsic deep learning approach to processing 3D meshes is in great need. Unlike images, 3D meshes have irregular connectivity, requiring careful design to capture relations in the data. To utilize the topology information while staying robust under different triangulations, we propose to encode mesh connectivity using Laplacian spectral analysis, along with mesh feature aggregation blocks (MFABs) that can split the surface domain into local pooling patches and aggregate global information amongst them. We build a mesh hierarchy from fine to coarse using Laplacian spectral clustering, which is flexible under isometric transformations. Inside the MFABs there are pooling layers to collect local information and multi-layer perceptrons to compute vertex features of increasing complexity. To obtain the relationships among different clusters, we introduce a Correlation Net to compute a correlation matrix, which can aggregate the features globally by matrix multiplication with cluster features. Our network architecture is flexible enough to be used on meshes with different numbers of vertices. We conduct several experiments including shape segmentation and classification, and our method outperforms state-of-the-art algorithms for these tasks on the ShapeNet and COSEG datasets.